力扣5674“构造字典序最大的合并字符串”解题报告

这道题本身属于Medium难度，算法也简单，代码也不长。

但算法的正确性证明并不那么显然。这里是证明过程。

1. 题目

5674.构造字典序最大的合并字符串。

题意很简单，给定两个字符串，要你把它们合并成一个，找出字典序最大的合并串。

比如给定两个字符串cabaa和bcaaa，字典序最大的合并串是cbcabaaaaa。合并方式是：

1
2
3

c  abaa
cbcabaaaaa
 bc    aaa

2. 算法

贪心法。

将给定的两个串简称为“源串”（名为word1和word2），最终结果串称为“目标串”（名为merge）。

再将word1用掉某些开头的字符（添加到merge）后剩余的部分（总是word1的后缀串）称为word1剩余串，命名为left1。类似的有left2。

每次选择left1和left2中字典序比较大的那个，选择其第一个字符，从原串的开头移除，并放到merge中。

循环执行，直到两个源串都变成空串为止。

例如上面例子，算法步骤如下（加粗的是用于比较left1和left2字典序的前缀）：

3. 代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution {
public:
    string largestMerge(string word1, string word2) {
        int pos1 = 0;
        int pos2 = 0;
        string ans;
        while (pos1 < word1.size() && pos2 < word2.size()) {
            if (strcmp(word1.c_str() + pos1, word2.c_str() + pos2) > 0) {
                ans += word1[pos1++];
            } else {
                ans += word2[pos2++];
            }
        }
        ans += word1.substr(pos1, -1);
        ans += word2.substr(pos2, -1);
        return ans;
    }
};

4. 证明

将要证明的命题规范地说一遍，就是：

每次决定从left1还是left2的开头选取字符时，选择字典序比较大的串的首字符添加到merge，最终能获得最大字典序的merge。

为了方便描述，在下面举个具体的例子。

假设left1和left2从[0]到[s-1]都相同，[s]不同。不妨设left1[s]是'x'，left2[s]是'y'。

证明分两步。

第1步：证明在最大字典序合并方案（下称“最佳方案”）中，left2[s]一定比left1[s]先出现。

第2步：证明先走left2[0]一定能到达最佳方案，而走left1[0]不一定能到达最佳方案。

补充：比较left1和left2时，如果left1是left2的前缀，可以假想left1后面有若干'\0'。

4.1. 第一步，证明：在最大字典序合并方案（下称“最佳方案”）中，left[s]一定比left[s]先出现

反证法。

假设left1[s]也就是'x'先出现。即，合并串中出现left1[s]时（left1走完s+1个字符），left2[s]尚未出现（left2走完的字符数k满足k <= s）。

1
2

                                               'x'
merge[0], merge[1], ..., merge[s + k - 1], merge[s + k], ...

在合并串中，前s + k个字符，是由

1
2

left1[0], left1[1], ..., left1[k - 1], ..., left1[s - 1]
left2[0], left2[1], ..., left2[k - 1]

构成的。根据定义，上下两串的[0]到[k - 1]是相同的。

对于假设中的合并方案，如果完全交换left1和left2的选择方案（即原方案中选择left1[0]的时候改成选择left2[0]，反之亦然），则merge[0]到merge[s + k - 1]将完全一致，区别仅仅是merge[s + k]可以是’y’。

易见，根据字典序的定义，新方案的字典序比原方案大。这就证明了原假设错误。证毕。

4.2. 第二步，证明：先选left2[0]一定能得到最大字典序的merge，先选left1[0]不一定能得到最大字典序的merge

注意下图：

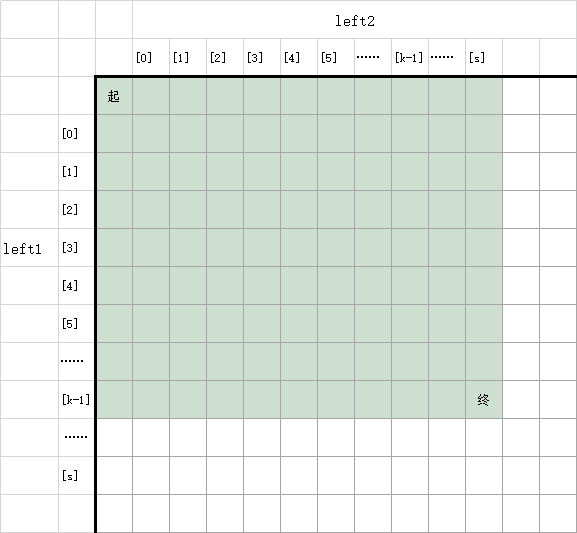
左上角是left1和left2都还没用过的情况。右下角是left1用了k个字符，left2用了s + 1个字符（最后一个字符是'y'）。

可以将两个字符串的合并看做从左上角到右下角的一个路径，每次只能往右或往下走。

假设对于left1和left2，走完前s + k + 1个字符的最佳方案是下图这样的：

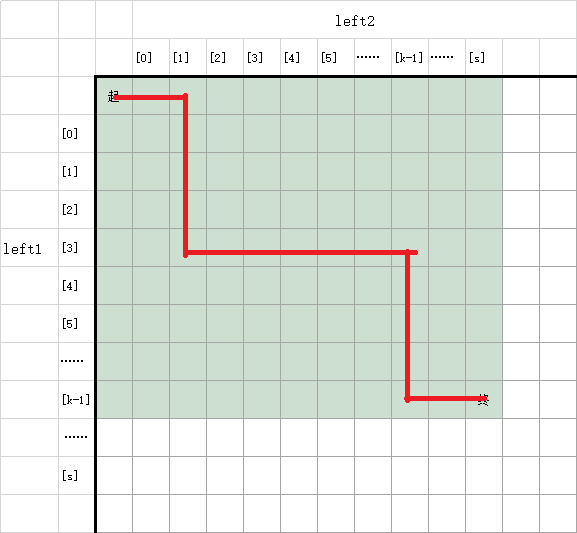
容易发现，由于left1和left2前s个字符相同（第s+1个字符不同），那么前k个字符必然相同。所以，经过对角线的路径，均可替换成其镜像路径，而不改变merge的值。如下图。

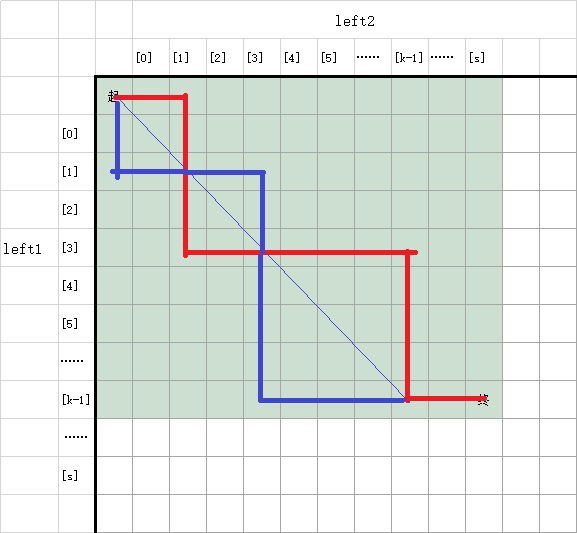
显然左上角的起点在对角线上。

如果在遇到字符left2[s]即'y'之前，路径最后一次经过对角线的位置是在起点之外的某个地方，那么从起点开始第一步往下走（选择left1[0]）还是往右走（选择left2[0]）均不影响达到最佳路径。即往右走是可以的。

而，如果路径最后一次（也是唯一一次）经过对角线的路径就是起点，如下图：

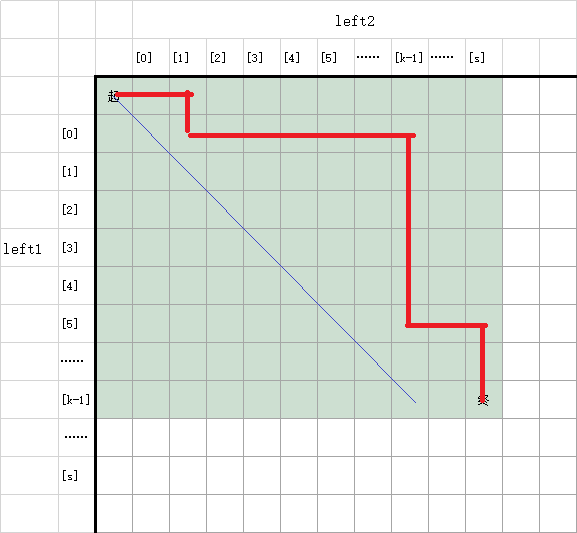
那么第一步就一定要往右走（选择left2[0]）。如果第一步往下走（选择left1[0]），因为路径不经过对角线，那就再也不可能到达目标格了。所以第一步不能往下走。

证毕。